Vector3 | space3

Brief

Vector3 represents 3D vectors as a set of three numerical components. It implements Vector interface.

Main features

Array like access u[0], u[1], ...
Algebra add, mul, neg
Geometry angle, cross, dist, rot, ...
Coordinates system accessors x, y, z, r, theta, lat, lon ...
Basis generators like ex, er(u), e(k), ...

Getting Started

Vector3 objects are made of an array of three cartesian coordinates in an arbitrary basis [x, y, z]. They can be considered the following column vector :

Vector3 shape

Coordinates systems

Before explaining any code lets start by understanding a little diagram.

Coordinates system

This diagram represents 3D space provided with an orthonormal basis, we see that u can be decomposed in three different coordinates systems :

cartesian coordinates (x, y, z)
cylindrical coordinates (rxy, theta, z)
spherical coordinates (r, theta, phi)

Note θ and Φ are respectively denoted theta and phi in the framework

The diagram specifies which convention are chosen for the coordinates systems provided.

You can use the coordinates accessors to get and set the value of the coordinates.

Example

let u = Vector3.ones; // u = (1, 1, 1)
u.r; // +sqrt(3)
u.x = 1; // 1
u.theta; // +pi/4
u.xyz; // [1, 1, 1]
u.r = 1; // u = 1/sqrt(3) * (1, 1, 1)

Geometrical features

Perform rotations, compute angles, cross product, ...

Example

let u = Vector3.ones, ex = Vector3.ex; // (1, 1, 1) (1, 0, 0)
u.angle(ex); // +pi/4
ex.cross(ex); // (0, 0, 0)
ex.rotZ(Math.PI / 2); // ex becomes ey

If you want to get deep into rotation features see Object3.

Standard basis

Represent the standard basis of 3D space made of :

ex = (1, 0, 0)
ey = (0, 1, 0)
ez = (0, 0, 1)

You can represent the basis (ex, ey, ez) on the following diagram :

Cartesian system

ex, ey and ez often respectively represents left, up and forward directions in computer graphics.

Anyway the first notation seems more general because math equations often use it without necessarily referring to these particular directions.

For example ex, ey, ez as respectively right, forward, up directions is often used in mechanics.

Note Here we have drawn ex, ey and ez as respectively right, forward, up.

You can then generate vectors of this standard basis

Example

let ex = Vector3.ex, ey = Vector3.ey, ez = Vector3.ez;

Spherical and cylindrical basis

The spherical basis vectors at u is represented bellow. Spherical system

Note All the vector of a local basis are orthogonal to each other and of norm 1.

You can generate or compute a local basis vector of the two coordinates systems.

Example

let er = Vector3.er(u), etheta = Vector3.etheta(u);
w = w.erxy(Vector3.ones) // w = 1/sqrt(2) * (1, 1, 0);

Hierarchy

Float64Array
- Vector3
  - Point3

Implements

Indexable

[index: number]: number

Brief

Vector3 represents 3D vectors as a set of three numerical components. It implements Vector interface.

Main features

Array like access u[0], u[1], ...
Algebra add, mul, neg
Geometry angle, cross, dist, rot, ...
Coordinates system accessors x, y, z, r, theta, lat, lon ...
Basis generators like ex, er(u), e(k), ...

Getting Started

Vector3 objects are made of an array of three cartesian coordinates in an arbitrary basis [x, y, z]. They can be considered the following column vector :

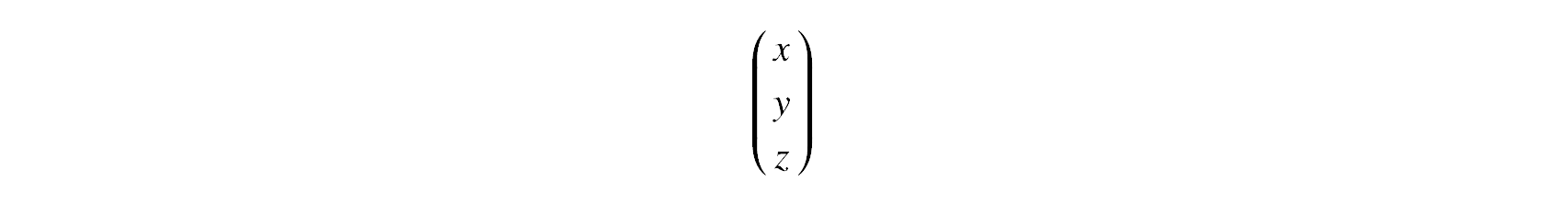
Vector3 shape

Coordinates systems

Before explaining any code lets start by understanding a little diagram.

Coordinates system

This diagram represents 3D space provided with an orthonormal basis, we see that u can be decomposed in three different coordinates systems :

cartesian coordinates (x, y, z)
cylindrical coordinates (rxy, theta, z)
spherical coordinates (r, theta, phi)

Note θ and Φ are respectively denoted theta and phi in the framework

The diagram specifies which convention are chosen for the coordinates systems provided.

You can use the coordinates accessors to get and set the value of the coordinates.

Example

let u = Vector3.ones; // u = (1, 1, 1)
u.r; // +sqrt(3)
u.x = 1; // 1
u.theta; // +pi/4
u.xyz; // [1, 1, 1]
u.r = 1; // u = 1/sqrt(3) * (1, 1, 1)

Geometrical features

Perform rotations, compute angles, cross product, ...

Example

let u = Vector3.ones, ex = Vector3.ex; // (1, 1, 1) (1, 0, 0)
u.angle(ex); // +pi/4
ex.cross(ex); // (0, 0, 0)
ex.rotZ(Math.PI / 2); // ex becomes ey

If you want to get deep into rotation features see Object3.

Standard basis

Represent the standard basis of 3D space made of :

ex = (1, 0, 0)
ey = (0, 1, 0)
ez = (0, 0, 1)

You can represent the basis (ex, ey, ez) on the following diagram :

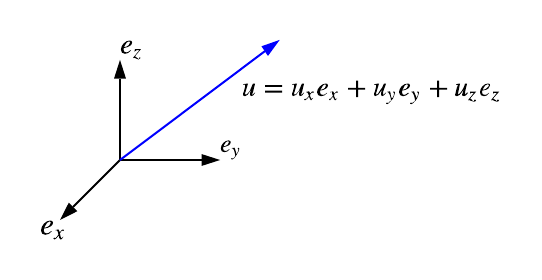
Cartesian system

ex, ey and ez often respectively represents left, up and forward directions in computer graphics.

Anyway the first notation seems more general because math equations often use it without necessarily referring to these particular directions.

For example ex, ey, ez as respectively right, forward, up directions is often used in mechanics.

Note Here we have drawn ex, ey and ez as respectively right, forward, up.

You can then generate vectors of this standard basis

Example

let ex = Vector3.ex, ey = Vector3.ey, ez = Vector3.ez;

Spherical and cylindrical basis

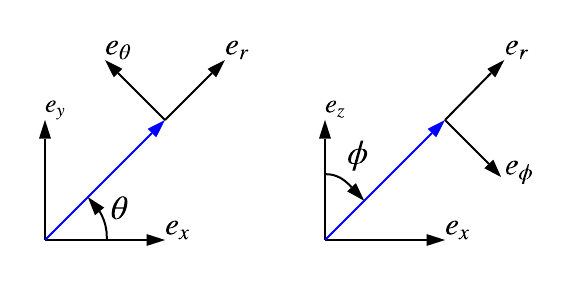
The spherical basis vectors at u is represented bellow. Spherical system

Note All the vector of a local basis are orthogonal to each other and of norm 1.

You can generate or compute a local basis vector of the two coordinates systems.

Example

let er = Vector3.er(u), etheta = Vector3.etheta(u);
w = w.erxy(Vector3.ones) // w = 1/sqrt(2) * (1, 1, 0);

Index

Constructors

constructor

Properties

Accessors

Methods

Constructors

constructor

new Vector3(x?: number, y?: number, z?: number): Vector3

- Defined in Vector3.ts:242
brief

Constructs a vector with cartesian coordinates. `

details

If you don't specify components then the underlying array is initialized with the default values for Float64Array.

Parameters
- Optional x: number
- Optional y: number
- Optional z: number
Returns Vector3

Properties

BYTES_PER_ELEMENT

BYTES_PER_ELEMENT: number

The size in bytes of each element in the array.

__@toStringTag

__@toStringTag: "Float64Array"

buffer

buffer: ArrayBufferLike

The ArrayBuffer instance referenced by the array.

byteLength

byteLength: number

The length in bytes of the array.

byteOffset

byteOffset: number

The offset in bytes of the array.

dim

dim: Readonly<number> = 3

length

length: number

The length of the array.

Static Float64Array

Float64Array: Float64ArrayConstructor

Accessors

lat

get lat(): number
set lat(newLat: number): void

- Defined in Vector3.ts:201
latitude of the vector in radians

Returns number
- Defined in Vector3.ts:205
latitude of the vector in radians

Parameters
- newLat: number
Returns void

lon

get lon(): number
set lon(newLon: number): void

- Defined in Vector3.ts:210
longitude of the vector in radians

Returns number
- Defined in Vector3.ts:215
longitude of the vector in radians

Parameters
- newLon: number
Returns void

mag

get mag(): number

- Defined in Vector3.ts:152
length of the vector

Returns number

mag2

get mag2(): number

- Defined in Vector3.ts:157
squared length of the vector

Returns number

phi

get phi(): number
set phi(newPhi: number): void

- Defined in Vector3.ts:183
third spherical coordinate, clockwise angle formed with ez in radians

Returns number
- Defined in Vector3.ts:187
third spherical coordinate, clockwise angle formed with ez in radians

Parameters
- newPhi: number
Returns void

r

get r(): number
set r(newR: number): void

- Defined in Vector3.ts:162
first spherical coordinate, length of the vector

Returns number
- Defined in Vector3.ts:166
first spherical coordinate, length of the vector

Parameters
- newR: number
Returns void

rthph

get rthph(): [number, number, number]
set rthph(coordinates: [number, number, number]): void

- Defined in Vector3.ts:232
spherical coordinates of the vector

Returns [number, number, number]
- Defined in Vector3.ts:236
spherical coordinates of the vector

Parameters
- coordinates: [number, number, number]
Returns void

rthz

get rthz(): [number, number, number]
set rthz(coordinates: [number, number, number]): void

- Defined in Vector3.ts:220
cylindrical coordinates of the vector

Returns [number, number, number]
- Defined in Vector3.ts:224
cylindrical coordinates of the vector

Parameters
- coordinates: [number, number, number]
Returns void

rxy

get rxy(): number
set rxy(newRxy: number): void

- Defined in Vector3.ts:192
first cylindrical coordinate, length of the projection of the vector on the plane formed with ex, ey

Returns number
- Defined in Vector3.ts:196
first cylindrical coordinate, length of the projection of the vector on the plane formed with ex, ey

Parameters
- newRxy: number
Returns void

theta

get theta(): number
set theta(newTheta: number): void

- Defined in Vector3.ts:174
second cylindrical and spherical coordinate, counterclockwise angle formed with ex in radians

Returns number
- Defined in Vector3.ts:178
second cylindrical and spherical coordinate, counterclockwise angle formed with ex in radians

Parameters
- newTheta: number
Returns void

x

get x(): number
set x(newX: number): void

- Defined in Vector3.ts:116
first cartesian coordinate

Returns number
- Defined in Vector3.ts:120
first cartesian coordinate

Parameters
- newX: number
Returns void

xyz

get xyz(): [number, number, number]
set xyz(coordinates: [number, number, number]): void

- Defined in Vector3.ts:143
cartesian coordinates of the vector

Returns [number, number, number]
- Defined in Vector3.ts:147
cartesian coordinates of the vector

Parameters
- coordinates: [number, number, number]
Returns void

y

get y(): number
set y(newY: number): void

- Defined in Vector3.ts:125
second cartesian coordinate

Returns number
- Defined in Vector3.ts:129
second cartesian coordinate

Parameters
- newY: number
Returns void

z

get z(): number
set z(newZ: number): void

- Defined in Vector3.ts:134
third cartesian coordinate

Returns number
- Defined in Vector3.ts:138
third cartesian coordinate

Parameters
- newZ: number
Returns void

Static dim

get dim(): number

- Defined in Vector3.ts:770
Returns number

Static ex

get ex(): Vector3

- Defined in Vector3.ts:810
Returns Vector3

Static exn

get exn(): Vector3

- Defined in Vector3.ts:816
opposite of the first vector of standard basis (-1, 0, 0)

Returns Vector3

Static ey

get ey(): Vector3

- Defined in Vector3.ts:821
second vector of standard basis (0, 1, 0)

Returns Vector3

Static eyn

get eyn(): Vector3

- Defined in Vector3.ts:826
opposite of the second vector of standard basis (0, -1, 0)

Returns Vector3

Static ez

get ez(): Vector3

- Defined in Vector3.ts:831
third vector of standard basis (0, 0, 1)

Returns Vector3

Static ezn

get ezn(): Vector3

- Defined in Vector3.ts:836
third vector of standard basis (0, 0, -1)

Returns Vector3

Static ones

get ones(): Vector3

- Defined in Vector3.ts:780
vector filled with 1

Returns Vector3

Static zeros

get zeros(): Vector3

- Defined in Vector3.ts:775
vector filled with 0

Returns Vector3

Methods

__@iterator

__@iterator(): IterableIterator<number>

Implementation of Vector.__@iterator

Inherited from Float64Array.[Symbol.iterator]
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es2015.iterable.d.ts:468
Returns IterableIterator<number>

abs

abs(): this

Implementation of Vector.abs
- Defined in Vector3.ts:354
Returns this

absc

absc(): Vector3

Implementation of Vector.absc
- Defined in Vector3.ts:361
Returns Vector3

add

add(u: Vector): this

Implementation of Vector.add
- Defined in Vector3.ts:411
Parameters
- u: Vector
Returns this

addc

addc(u: Vector): Vector3

Implementation of Vector.addc
- Defined in Vector3.ts:418
Parameters
- u: Vector
Returns Vector3

angle

angle(u: Vector): number

- Defined in Vector3.ts:694
unsigned angle between two vectors in radians

Parameters
- u: Vector
Returns number

area

area(u: Vector): number

- Defined in Vector3.ts:679
area of the parallelepiped formed with the two vectors

Parameters
- u: Vector
Returns number

array

array(): number[]

Implementation of Vector.array
- Defined in Vector3.ts:263
Returns number[]

assign

assign(x: number, y: number, z: number): this

- Defined in Vector3.ts:267
Parameters
- x: number
- y: number
- z: number
Returns this

berp

berp(u: Vector, u1: Vector, u2: Vector, s: number): this

Implementation of Vector.berp
- Defined in Vector3.ts:504
Parameters
- u: Vector
- u1: Vector
- u2: Vector
- s: number
Returns this

berpc

berpc(u: Vector, u1: Vector, u2: Vector, s: number): Vector3

Implementation of Vector.berpc
- Defined in Vector3.ts:518
Parameters
- u: Vector
- u1: Vector
- u2: Vector
- s: number
Returns Vector3

ceil

ceil(): this

Implementation of Vector.ceil
- Defined in Vector3.ts:319
Returns this

ceilc

ceilc(): Vector3

Implementation of Vector.ceilc
- Defined in Vector3.ts:326
Returns Vector3

clone

clone(): Vector3

Implementation of Vector.clone
- Defined in Vector3.ts:281
Returns Vector3

comb

comb(s: number, u: Vector): this

Implementation of Vector.comb
- Defined in Vector3.ts:466
Parameters
- s: number
- u: Vector
Returns this

combc

combc(s: number, u: Vector): Vector3

Implementation of Vector.combc
- Defined in Vector3.ts:473
Parameters
- s: number
- u: Vector
Returns Vector3

copy

copy(u: Vector): this

Implementation of Vector.copy
- Defined in Vector3.ts:274
Parameters
- u: Vector
Returns this

copyWithin

copyWithin(target: number, start: number, end?: number): this

Implementation of Vector.copyWithin

Inherited from Float64Array.copyWithin
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3854
Returns the this object after copying a section of the array identified by start and end to the same array starting at position target

Parameters
- target: number
  
  If target is negative, it is treated as length+target where length is the length of the array.
- start: number
  
  If start is negative, it is treated as length+start. If end is negative, it is treated as length+end.
- Optional end: number
  
  If not specified, length of the this object is used as its default value.
Returns this

cos

cos(u: Vector): number

- Defined in Vector3.ts:699
cosine of the angle between two vector

Parameters
- u: Vector
Returns number

cross

cross(u: Vector): this

- Defined in Vector3.ts:661
cross product of two vector u x v

Parameters
- u: Vector
Returns this

crossc

crossc(u: Vector): Vector3

- Defined in Vector3.ts:674
Parameters
- u: Vector
Returns Vector3

der

der(ds: number, u: Vector): this

Implementation of Vector.der
- Defined in Vector3.ts:522
Parameters
- ds: number
- u: Vector
Returns this

derc

derc(ds: number, u: Vector): Vector3

Implementation of Vector.derc
- Defined in Vector3.ts:529
Parameters
- ds: number
- u: Vector
Returns Vector3

dist

dist(u: Vector): number

Implementation of Vector.dist
- Defined in Vector3.ts:560
Parameters
- u: Vector
Returns number

dist1

dist1(u: Vector): number

Implementation of Vector.dist1
- Defined in Vector3.ts:564
Parameters
- u: Vector
Returns number

dist2

dist2(u: Vector): number

Implementation of Vector.dist2
- Defined in Vector3.ts:571
Parameters
- u: Vector
Returns number

div

div(s: number): this

Implementation of Vector.div
- Defined in Vector3.ts:455
Parameters
- s: number
Returns this

divc

divc(s: number): Vector3

Implementation of Vector.divc
- Defined in Vector3.ts:462
Parameters
- s: number
Returns Vector3

dot

dot(u: Vector): number

Implementation of Vector.dot
- Defined in Vector3.ts:556
Parameters
- u: Vector
Returns number

entries

entries(): IterableIterator<[number, number]>

Implementation of Vector.entries

Inherited from Float64Array.entries
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es2015.iterable.d.ts:472
Returns an array of key, value pairs for every entry in the array

Returns IterableIterator<[number, number]>

ephi

ephi(u: Vector): this

- Defined in Vector3.ts:743
Parameters
- u: Vector
Returns this

equal1

equal1(u: Vector): boolean

Implementation of Vector.equal1
- Defined in Vector3.ts:582
Parameters
- u: Vector
Returns boolean

equal2

equal2(u: Vector): boolean

Implementation of Vector.equal2
- Defined in Vector3.ts:594
Parameters
- u: Vector
Returns boolean

er

er(u: Vector): this

- Defined in Vector3.ts:715
Parameters
- u: Vector
Returns this

erxy

erxy(u: Vector): this

- Defined in Vector3.ts:726
Parameters
- u: Vector
Returns this

etheta

etheta(u: Vector): this

- Defined in Vector3.ts:735
Parameters
- u: Vector
Returns this

every

every(callbackfn: function, thisArg?: any): boolean

Inherited from Float64Array.every
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3864
Determines whether all the members of an array satisfy the specified test.

Parameters
- callbackfn: function
  
  A function that accepts up to three arguments. The every method calls the callbackfn function for each element in array1 until the callbackfn returns false, or until the end of the array.
  - - (value: number, index: number, array: Float64Array): boolean
    - Parameters
      - value: number
      - index: number
      - array: Float64Array
      Returns boolean
- Optional thisArg: any
  
  An object to which the this keyword can refer in the callbackfn function. If thisArg is omitted, undefined is used as the this value.
Returns boolean

exact

exact(u: Vector): boolean

Implementation of Vector.exact
- Defined in Vector3.ts:578
Parameters
- u: Vector
Returns boolean

fill

fill(s: number): this

Implementation of Vector.fill

Overrides Float64Array.fill
- Defined in Vector3.ts:388
Parameters
- s: number
Returns this

fillc

fillc(s: number): Vector3

Implementation of Vector.fillc
- Defined in Vector3.ts:395
Parameters
- s: number
Returns Vector3

filter

filter(callbackfn: function, thisArg?: any): Float64Array

Inherited from Float64Array.filter
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3883
Returns the elements of an array that meet the condition specified in a callback function.

Parameters
- callbackfn: function
  
  A function that accepts up to three arguments. The filter method calls the callbackfn function one time for each element in the array.
  - - (value: number, index: number, array: Float64Array): any
    - Parameters
      - value: number
      - index: number
      - array: Float64Array
      Returns any
- Optional thisArg: any
  
  An object to which the this keyword can refer in the callbackfn function. If thisArg is omitted, undefined is used as the this value.
Returns Float64Array

find

find(predicate: function, thisArg?: any): number | undefined

Inherited from Float64Array.find
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3894
Returns the value of the first element in the array where predicate is true, and undefined otherwise.

Parameters
- predicate: function
  
  find calls predicate once for each element of the array, in ascending order, until it finds one where predicate returns true. If such an element is found, find immediately returns that element value. Otherwise, find returns undefined.
  - - (value: number, index: number, obj: Float64Array): boolean
    - Parameters
      - value: number
      - index: number
      - obj: Float64Array
      Returns boolean
- Optional thisArg: any
  
  If provided, it will be used as the this value for each invocation of predicate. If it is not provided, undefined is used instead.
Returns number | undefined

findIndex

findIndex(predicate: function, thisArg?: any): number

Inherited from Float64Array.findIndex
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3905
Returns the index of the first element in the array where predicate is true, and -1 otherwise.

Parameters
- predicate: function
  
  find calls predicate once for each element of the array, in ascending order, until it finds one where predicate returns true. If such an element is found, findIndex immediately returns that element index. Otherwise, findIndex returns -1.
  - - (value: number, index: number, obj: Float64Array): boolean
    - Parameters
      - value: number
      - index: number
      - obj: Float64Array
      Returns boolean
- Optional thisArg: any
  
  If provided, it will be used as the this value for each invocation of predicate. If it is not provided, undefined is used instead.
Returns number

floor

floor(): this

Implementation of Vector.floor
- Defined in Vector3.ts:308
Returns this

floorc

floorc(): Vector3

Implementation of Vector.floorc
- Defined in Vector3.ts:315
Returns Vector3

forEach

forEach(callbackfn: function, thisArg?: any): void

Inherited from Float64Array.forEach
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3914
Performs the specified action for each element in an array.

Parameters
- callbackfn: function
  
  A function that accepts up to three arguments. forEach calls the callbackfn function one time for each element in the array.
  - - (value: number, index: number, array: Float64Array): void
    - Parameters
      - value: number
      - index: number
      - array: Float64Array
      Returns void
- Optional thisArg: any
  
  An object to which the this keyword can refer in the callbackfn function. If thisArg is omitted, undefined is used as the this value.
Returns void

gaussian

gaussian(xm: number, ym: number, zm: number, xd: number, yd?: number, zd?: number): this

- Defined in Vector3.ts:763
brief

random vector following normal law

details

If yd and zd are unspecified then xd will represent the standard deviation for all axis.

Parameters
- xm: number
  
  average value of x
- ym: number
  
  average value of y
- zm: number
  
  average value of z
- xd: number
  
  standard deviation along x axis
- Default value yd: number = xd
  
  standard deviation along y axis
- Default value zd: number = xd
  
  standard deviation along z axis
Returns this

herp

herp(u: Vector, u1: Vector, u2: Vector, s: number): this

Implementation of Vector.herp
- Defined in Vector3.ts:488
Parameters
- u: Vector
- u1: Vector
- u2: Vector
- s: number
Returns this

herpc

herpc(u: Vector, u1: Vector, u2: Vector, s: number): Vector3

Implementation of Vector.herpc
- Defined in Vector3.ts:500
Parameters
- u: Vector
- u1: Vector
- u2: Vector
- s: number
Returns Vector3

includes

includes(searchElement: number, fromIndex?: number): boolean

Implementation of Vector.includes

Inherited from Float64Array.includes
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es2016.array.include.d.ts:117
Determines whether an array includes a certain element, returning true or false as appropriate.

Parameters
- searchElement: number
  
  The element to search for.
- Optional fromIndex: number
  
  The position in this array at which to begin searching for searchElement.
Returns boolean

indexOf

indexOf(searchElement: number, fromIndex?: number): number

Implementation of Vector.indexOf

Inherited from Float64Array.indexOf
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3922
Returns the index of the first occurrence of a value in an array.

Parameters
- searchElement: number
  
  The value to locate in the array.
- Optional fromIndex: number
  
  The array index at which to begin the search. If fromIndex is omitted, the search starts at index 0.
Returns number

inv

inv(): this

Implementation of Vector.inv
- Defined in Vector3.ts:545
Returns this

invc

invc(): Vector3

Implementation of Vector.invc
- Defined in Vector3.ts:552
Returns Vector3

join

join(separator?: string): string

Implementation of Vector.join

Inherited from Float64Array.join
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3929
Adds all the elements of an array separated by the specified separator string.

Parameters
- Optional separator: string
  
  A string used to separate one element of an array from the next in the resulting String. If omitted, the array elements are separated with a comma.
Returns string

keys

keys(): IterableIterator<number>

Implementation of Vector.keys

Inherited from Float64Array.keys
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es2015.iterable.d.ts:476
Returns an list of keys in the array

Returns IterableIterator<number>

lastIndexOf

lastIndexOf(searchElement: number, fromIndex?: number): number

Implementation of Vector.lastIndexOf

Inherited from Float64Array.lastIndexOf
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3937
Returns the index of the last occurrence of a value in an array.

Parameters
- searchElement: number
  
  The value to locate in the array.
- Optional fromIndex: number
  
  The array index at which to begin the search. If fromIndex is omitted, the search starts at index 0.
Returns number

lerp

lerp(u: Vector, s: number): this

Implementation of Vector.lerp
- Defined in Vector3.ts:477
Parameters
- u: Vector
- s: number
Returns this

lerpc

lerpc(u: Vector, s: number): Vector3

Implementation of Vector.lerpc
- Defined in Vector3.ts:484
Parameters
- u: Vector
- s: number
Returns Vector3

map

map(callbackfn: function, thisArg?: any): Float64Array

Inherited from Float64Array.map
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3952
Calls a defined callback function on each element of an array, and returns an array that contains the results.

Parameters
- callbackfn: function
  
  A function that accepts up to three arguments. The map method calls the callbackfn function one time for each element in the array.
  - - (value: number, index: number, array: Float64Array): number
    - Parameters
      - value: number
      - index: number
      - array: Float64Array
      Returns number
- Optional thisArg: any
  
  An object to which the this keyword can refer in the callbackfn function. If thisArg is omitted, undefined is used as the this value.
Returns Float64Array

max

max(u: Vector): this

Implementation of Vector.max
- Defined in Vector3.ts:377
Parameters
- u: Vector
Returns this

maxc

maxc(u: Vector): Vector3

Implementation of Vector.maxc
- Defined in Vector3.ts:384
Parameters
- u: Vector
Returns Vector3

min

min(u: Vector): this

Implementation of Vector.min
- Defined in Vector3.ts:365
Parameters
- u: Vector
Returns this

minc

minc(u: Vector): Vector3

Implementation of Vector.minc
- Defined in Vector3.ts:372
Parameters
- u: Vector
Returns Vector3

mul

mul(s: number): this

Implementation of Vector.mul
- Defined in Vector3.ts:444
Parameters
- s: number
Returns this

mulc

mulc(s: number): Vector3

Implementation of Vector.mulc
- Defined in Vector3.ts:451
Parameters
- s: number
Returns Vector3

neg

neg(): this

Implementation of Vector.neg
- Defined in Vector3.ts:433
Returns this

negc

negc(): Vector3

Implementation of Vector.negc
- Defined in Vector3.ts:440
Returns Vector3

nil

nil(): boolean

Implementation of Vector.nil
- Defined in Vector3.ts:598
Returns boolean

norm

norm(): this

Implementation of Vector.norm
- Defined in Vector3.ts:399
Returns this

normc

normc(): Vector3

Implementation of Vector.normc
- Defined in Vector3.ts:407
Returns Vector3

prod

prod(u: Vector): this

Implementation of Vector.prod
- Defined in Vector3.ts:534
Hadamard product of two vectors

Parameters
- u: Vector
Returns this

prodc

prodc(u: Vector): Vector3

Implementation of Vector.prodc
- Defined in Vector3.ts:541
Parameters
- u: Vector
Returns Vector3

random

random(): this

Implementation of Vector.random
- Defined in Vector3.ts:301
Returns this

reduce

reduce(callbackfn: function): number
reduce(callbackfn: function, initialValue: number): number
reduce<U>(callbackfn: function, initialValue: U): U

Inherited from Float64Array.reduce
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3964
Calls the specified callback function for all the elements in an array. The return value of the callback function is the accumulated result, and is provided as an argument in the next call to the callback function.

Parameters
- callbackfn: function
  
  A function that accepts up to four arguments. The reduce method calls the callbackfn function one time for each element in the array.
  - - (previousValue: number, currentValue: number, currentIndex: number, array: Float64Array): number
    - Parameters
      - previousValue: number
      - currentValue: number
      - currentIndex: number
      - array: Float64Array
      Returns number
Returns number
Inherited from Float64Array.reduce
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3965
Parameters
- callbackfn: function
  - - (previousValue: number, currentValue: number, currentIndex: number, array: Float64Array): number
    - Parameters
      - previousValue: number
      - currentValue: number
      - currentIndex: number
      - array: Float64Array
      Returns number
- initialValue: number
Returns number
Inherited from Float64Array.reduce
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3977
Calls the specified callback function for all the elements in an array. The return value of the callback function is the accumulated result, and is provided as an argument in the next call to the callback function.

Type parameters
- U
Parameters
- callbackfn: function
  
  A function that accepts up to four arguments. The reduce method calls the callbackfn function one time for each element in the array.
  - - (previousValue: U, currentValue: number, currentIndex: number, array: Float64Array): U
    - Parameters
      - previousValue: U
      - currentValue: number
      - currentIndex: number
      - array: Float64Array
      Returns U
- initialValue: U
  
  If initialValue is specified, it is used as the initial value to start the accumulation. The first call to the callbackfn function provides this value as an argument instead of an array value.
Returns U

reduceRight

reduceRight(callbackfn: function): number
reduceRight(callbackfn: function, initialValue: number): number
reduceRight<U>(callbackfn: function, initialValue: U): U

Inherited from Float64Array.reduceRight
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3989
Calls the specified callback function for all the elements in an array, in descending order. The return value of the callback function is the accumulated result, and is provided as an argument in the next call to the callback function.

Parameters
- callbackfn: function
  
  A function that accepts up to four arguments. The reduceRight method calls the callbackfn function one time for each element in the array.
  - - (previousValue: number, currentValue: number, currentIndex: number, array: Float64Array): number
    - Parameters
      - previousValue: number
      - currentValue: number
      - currentIndex: number
      - array: Float64Array
      Returns number
Returns number
Inherited from Float64Array.reduceRight
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:3990
Parameters
- callbackfn: function
  - - (previousValue: number, currentValue: number, currentIndex: number, array: Float64Array): number
    - Parameters
      - previousValue: number
      - currentValue: number
      - currentIndex: number
      - array: Float64Array
      Returns number
- initialValue: number
Returns number
Inherited from Float64Array.reduceRight
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4002
Calls the specified callback function for all the elements in an array, in descending order. The return value of the callback function is the accumulated result, and is provided as an argument in the next call to the callback function.

Type parameters
- U
Parameters
- callbackfn: function
  
  A function that accepts up to four arguments. The reduceRight method calls the callbackfn function one time for each element in the array.
  - - (previousValue: U, currentValue: number, currentIndex: number, array: Float64Array): U
    - Parameters
      - previousValue: U
      - currentValue: number
      - currentIndex: number
      - array: Float64Array
      Returns U
- initialValue: U
  
  If initialValue is specified, it is used as the initial value to start the accumulation. The first call to the callbackfn function provides this value as an argument instead of an array value.
Returns U

reset0

reset0(): this

Implementation of Vector.reset0
- Defined in Vector3.ts:286
sets vector to zeros

Returns this

reset1

reset1(): this

Implementation of Vector.reset1
- Defined in Vector3.ts:294
sets vector to ones

Returns this

reverse

reverse(): Float64Array

Implementation of Vector.reverse

Inherited from Float64Array.reverse
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4007
Reverses the elements in an Array.

Returns Float64Array

rot

rot(u: Vector, theta: number, cos?: cos, sin?: sin): this

- Defined in Vector3.ts:643
See Object3 for more details

Parameters
- u: Vector
- theta: number
- Default value cos: cos = Math.cos
- Default value sin: sin = Math.sin
Returns this

rotX

rotX(theta: number, cos?: cos, sin?: sin): this

- Defined in Vector3.ts:619
See Object3 for more details

Parameters
- theta: number
- Default value cos: cos = Math.cos
- Default value sin: sin = Math.sin
Returns this

rotY

rotY(theta: number, cos?: cos, sin?: sin): this

- Defined in Vector3.ts:627
See Object3 for more details

Parameters
- theta: number
- Default value cos: cos = Math.cos
- Default value sin: sin = Math.sin
Returns this

rotZ

rotZ(theta: number, cos?: cos, sin?: sin): this

- Defined in Vector3.ts:635
See Object3 for more details

Parameters
- theta: number
- Default value cos: cos = Math.cos
- Default value sin: sin = Math.sin
Returns this

round

round(): this

Implementation of Vector.round
- Defined in Vector3.ts:331
Returns this

roundc

roundc(): Vector3

Implementation of Vector.roundc
- Defined in Vector3.ts:338
Returns Vector3

set

set(array: ArrayLike<number>, offset?: number): void

Implementation of Vector.set

Inherited from Float64Array.set
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4014
Sets a value or an array of values.

Parameters
- array: ArrayLike<number>
  
  A typed or untyped array of values to set.
- Optional offset: number
  
  The index in the current array at which the values are to be written.
Returns void

slice

slice(start?: number, end?: number): Float64Array

Implementation of Vector.slice

Inherited from Float64Array.slice
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4021
Returns a section of an array.

Parameters
- Optional start: number
  
  The beginning of the specified portion of the array.
- Optional end: number
  
  The end of the specified portion of the array.
Returns Float64Array

some

some(callbackfn: function, thisArg?: any): boolean

Inherited from Float64Array.some
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4031
Determines whether the specified callback function returns true for any element of an array.

Parameters
- callbackfn: function
  
  A function that accepts up to three arguments. The some method calls the callbackfn function for each element in array1 until the callbackfn returns true, or until the end of the array.
  - - (value: number, index: number, array: Float64Array): boolean
    - Parameters
      - value: number
      - index: number
      - array: Float64Array
      Returns boolean
- Optional thisArg: any
  
  An object to which the this keyword can refer in the callbackfn function. If thisArg is omitted, undefined is used as the this value.
Returns boolean

sort

sort(compareFn?: function): this

Inherited from Float64Array.sort
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4038
Sorts an array.

Parameters
- Optional compareFn: function
  
  The name of the function used to determine the order of the elements. If omitted, the elements are sorted in ascending, ASCII character order.
  - - (a: number, b: number): number
    - Parameters
      - a: number
      - b: number
      Returns number
Returns this

string

string(): string

Implementation of Vector.string
- Defined in Vector3.ts:259
Returns string

sub

sub(u: Vector): this

Implementation of Vector.sub
- Defined in Vector3.ts:422
Parameters
- u: Vector
Returns this

subarray

subarray(begin: number, end?: number): Float64Array

Implementation of Vector.subarray

Inherited from Float64Array.subarray
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4046
Gets a new Float64Array view of the ArrayBuffer store for this array, referencing the elements at begin, inclusive, up to end, exclusive.

Parameters
- begin: number
  
  The index of the beginning of the array.
- Optional end: number
  
  The index of the end of the array.
Returns Float64Array

subc

subc(u: Vector): Vector3

Implementation of Vector.subc
- Defined in Vector3.ts:429
Parameters
- u: Vector
Returns Vector3

toLocaleString

toLocaleString(): string

Implementation of Vector.toLocaleString

Inherited from Float64Array.toLocaleString
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4051
Converts a number to a string by using the current locale.

Returns string

toString

toString(): string

Implementation of Vector.toString

Inherited from Float64Array.toString
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es5.d.ts:4056
Returns a string representation of an array.

Returns string

trunc

trunc(decimals: number): this

Implementation of Vector.trunc
- Defined in Vector3.ts:342
Parameters
- decimals: number
Returns this

truncc

truncc(decimals: number): Vector3

Implementation of Vector.truncc
- Defined in Vector3.ts:350
Parameters
- decimals: number
Returns Vector3

values

values(): IterableIterator<number>

Implementation of Vector.values

Inherited from Float64Array.values
- Defined in /home/travis/build/samiBendou/space3/node_modules/typedoc/node_modules/typescript/lib/lib.es2015.iterable.d.ts:480
Returns an list of values in the array

Returns IterableIterator<number>

zero1

zero1(): boolean

Implementation of Vector.zero1
- Defined in Vector3.ts:602
Returns boolean

zero2

zero2(): boolean

Implementation of Vector.zero2
- Defined in Vector3.ts:611
Returns boolean

Static array

array(arr: number[]): Vector3

- Defined in Vector3.ts:898
vector from coordinates of array in the form [x, y, z, ...]

Parameters
- arr: number[]
Returns Vector3

Static e

e(k: number): Vector3

- Defined in Vector3.ts:845
brief

standard basis vector

details

e(0) == ex, e(1) == ey, e(2) == ez.

Parameters
- k: number
  
  order of the vector in basis
Returns Vector3

Static en

en(k: number): Vector3

- Defined in Vector3.ts:856
brief

opposite of standard basis vector

details

en(0) == exn, en(1) == eyn, en(2) == ezn.

Parameters
- k: number
  
  order of the vector in basis
Returns Vector3

Static ephi

ephi(u: Vector): Vector3

- Defined in Vector3.ts:893
brief

normal vector of spherical basis

details

Normal vector is perpendicular to the radial vector and oriented in the positive phi direction.

Parameters
- u: Vector
  
  position of local basis
Returns Vector3

Static er

er(u: Vector): Vector3

- Defined in Vector3.ts:866
brief

radial vector of spherical basis

Parameters
- u: Vector
  
  position of local basis
Returns Vector3

Static erxy

erxy(u: Vector): Vector3

- Defined in Vector3.ts:874
brief

radial vector of cylindrical basis

Parameters
- u: Vector
  
  position of local basis
Returns Vector3

Static etheta

etheta(u: Vector): Vector3

- Defined in Vector3.ts:884
brief

prograde vector of spherical basis

details

Prograde vector is perpendicular to the radial vector and oriented in the positive theta direction. This vector also correspond to the prograde vector of cylindrical basis.

Parameters
- u: Vector
  
  position of local basis
Returns Vector3

Static gaussian

gaussian(xm: number, ym: number, zm: number, xd: number, yd?: number, zd?: number): Vector3

- Defined in Vector3.ts:795
vector with coordinates following gaussian law. See Vector3.gaussian for more details.

Parameters
- xm: number
- ym: number
- zm: number
- xd: number
- Default value yd: number = xd
- Default value zd: number = xd
Returns Vector3

Static random

random(): Vector3

- Defined in Vector3.ts:790
vector filled with uniform random values. See random for more details.

Returns Vector3

Static rthph

rthph(r: number, theta: number, phi: number): Vector3

- Defined in Vector3.ts:805
vector with given spherical coordinates. See rthph for more details.

Parameters
- r: number
- theta: number
- phi: number
Returns Vector3

Static rthz

rthz(rxy: number, theta: number, z: number): Vector3

- Defined in Vector3.ts:800
vector with given cylindrical coordinates. See [[this.rthz]] for more details.

Parameters
- rxy: number
- theta: number
- z: number
Returns Vector3

Static scalar

scalar(s: number): Vector3

- Defined in Vector3.ts:785
vector filled with s

Parameters
- s: number
Returns Vector3

Brief

Main features

Getting Started

Coordinates systems

Example

Geometrical features

Example

Standard basis

Example

Spherical and cylindrical basis

Example

Hierarchy

Implements

Indexable

Brief

Main features

Getting Started

Coordinates systems

Example

Geometrical features

Example

Standard basis

Example

Spherical and cylindrical basis

Example

Index

Constructors

Properties

Accessors

Methods

Constructors

constructor

Parameters

Optional x: number

Optional y: number

Optional z: number

Returns Vector3

Properties

BYTES_PER_ELEMENT

__@toStringTag

buffer

byteLength

byteOffset

dim

length

Static Float64Array

Accessors

lat

Returns number

Parameters

newLat: number

Returns void

lon

Returns number

Parameters

newLon: number

Returns void

mag

Returns number

mag2

Returns number

phi

Returns number

Parameters

newPhi: number

Returns void

r

Returns number

Parameters

newR: number

Returns void

rthph

Returns [number, number, number]

Parameters

coordinates: [number, number, number]

Returns void

rthz

Returns [number, number, number]

Parameters

coordinates: [number, number, number]